Cosmologia: A teoria do Big Bang – I
E não há criatura alguma encoberta diante dele; antes todas as coisas estão nuas e patentes aos olhos daquele com quem temos de tratar.
Hebreus 4:13
Finalmente chegamos na Grande Controvérsia na relação entre fé cristã em ciência! Na famigerada teoria que originou o mundo, o universo, a vida, os ETs! Aquela teoria que é odiada pelos detratores da Relatividade Geral (RG) e constantemente tem sido objeto de retalhamento, reconstrução e amor por outros físicos! A maldosa teoria que é deturpada pelos teólogos antigos que não conheciam os fundamentos de uma termodinâmica ou de simples observações astronômicas em um céu limpo! A tremenda teoria que é detonada atualmente por outros cristãos (por motivações legítimas) que não sabem (ou não lembram) da física newtoniana do ensino médio! A teoria odiada por pregadores (com intenção sincera) que tentam nos livrar das amarras satânicas do ateísmo! A teoria que é difamada por cosmólogos que, motivados por cosmovisões particulares, querem tirar quaisquer resquícios de criação ou de um agente criador do universo! A queridinha dos ateus militantes que adoram tirar Deus, Criador ou qualquer ser transcendental que dê ideia de início ou criação! Ela mesma, a teoria que é colocada como contrária às Escrituras por quem não conhece muito bem a literatura bíblica e a cosmologia atual!
O parágrafo anterior poderia ser continuado por páginas e páginas de contradições, destilações de ódio e um pouquinho de amor por parte de teólogos (sempre me referindo aos que estão dentro do cristianismo), ateus, cientistas e cristãos de forma geral. Toda essa descritiva é para falar, especificamente, sobre a teoria do Big Bang (que chamarei de BB)
Como leitor do CosmoTeo, você já deve ter quase todas as bases e fundamentos desse modelo cosmológico que tratarei especificamente aqui. Por exemplo, nessa série sobre cosmologia já mencionei sobre as controvérsias históricas sobre o tamanho do universo e cosmovisões de alguns cientistas que foram contrários ou favoráveis ao BB (isso mesmo: não há cientista isento ou imparcial no mundo da ciência). Só nesses 2 textos há muitos elementos que são basilares ao BB. E aqui, sintetizarei todos os fundamentos; talvez fique um pouquinho repetitivo, mas é um recurso didático que usarei para solidificar suas ideias sobre essa tão famosa (odiada e amada) teoria cosmológica.
Para nos situarmos na história: na coluna sobre os primórdios dos estudos do BB cheguei até os anos 1937, quando foi publicado o último artigo por Walker que monta a métrica de FLRW, que começou com os trabalhos da RG em 1916. Farei um breve resumo desse período histórico com foco na parte científica.
Em 1905, Einstein publica a Relatividade Especial (RE). Essa teoria trata, dentre outras coisas, sobre efeitos no espaço e no tempo quando a velocidade é relativística ou com percentuais consideráveis (>20%) comparados com a velocidade da luz (que é, arredondando, 300 mil km/s; por segundo e não por hora). Como se trata sobre referenciais inerciais (referencial que não tem ação externa de força, como força gravitacional, uma corda puxando ou uma mola; os movimentos são com velocidades constantes, sem aceleração), Einstein generaliza a RE para englobar referenciais não-inerciais e produz a RG. A ideia é ter forças atuando nos referenciais, como a gravitacional. Diversos resultados são derivados da RG e um deles é que a gravidade advém do efeito da curvatura do espaço-tempo.
Em 1922, o físico russo Friedman derivou um modelo cosmológico utilizando a RG. Ou seja, utilizando as equações da RG, ele deduziu como funcionaria um universo onde efeitos gravitacionais (curvaturas do espaço-tempo) dominariam. Ao fazer isso, Friedman descobre que o universo tem dinâmica: ele se expande ou se contrai, dependendo do conteúdo (matéria) e do volume (tamanho).
Cinco anos depois, o padre jesuíta e físico Lemaître publica um outro trabalho, parecido com o do Friedman, só que com uns pontos adicionais. Utilizando os dados publicados por Hubble sobre afastamento de galáxias em relação a nós, ele pôde refinar o modelo teórico sobre o universo e chegou à conclusão de que o universo poderia ter tipo um começo: estado quente, denso e um tamanho análogo a um ovo (cósmico). No início dos anos 1930 ainda estava nascendo a mecânica quântica e Lemaître observou que seria necessário a aplicação dela no início do universo: como tudo começa em um volume muito pequeno, então seria preciso considerar os efeitos quânticos da matéria. Isso acontece décadas antes do que conhecemos como cosmologia quântica (assunto que ainda trataremos futuramente).
Nesse meandro, a física do universo está se desenvolvendo por outros caminhos, como a mecânica quântica, a física estatística (ou termodinâmica) aplicada ao universo (Robertson e Walker utilizaram esses conceitos para montarem outras partes do BB) e a astronomia observacional. Este último ponto destaco os trabalhos de Hubble sobre a expansão do universo (afastamento das galáxias) e a solução da controvérsia de 1920. A “finalização” do modelo do BB é com os trabalhos de Robertson e Walker, em um total de 5 artigos entre 1935 e 1937.
Todos esses trabalhos podem ser resumidos em uma palavra: desenvolvimento da métrica de FLRW (Friedman-Lemaître-Robertson-Walker). Métrica é uma expressão que utilizamos na matemática e que significa, em palavras simples, a propriedade geométrica de um espaço. Vou explicar esse detalhe e observe atentamente cada palavra que utilizarei. Veja a figura abaixo:

Essa figura é a representação da geodésica: a menor distância entre 2 pontos (A e B). Observe que a geodésica está desenhada em uma superfície ou, como chamamos na escola, em uma geometria plana (euclidiana). Só que essa geodésica tem um nome especial: reta. Indo mais um pouco: a geodésica é uma curva de menor distância entre 2 pontos. O nome da curva, na geometria plana ou euclidiana, é reta. Sim, os termos estão certos: a reta é um caso particular de curva na geometria euclidiana.
A métrica é a “conta matemática” da geodésica. Ou seja, temos uma geodésica (a menor distância entre 2 pontos em uma geometria) e a métrica faz o cálculo de como é essa distância ou comportamento dessa geodésica na geometria (euclidiana, riemanniana etc). Pode até parecer contraintuitivo. Se precisar, releia esse pequeno trecho quantas vezes precisar ou pergunte-me que terei o prazer em responder com outras palavras ou exemplos.
Um exemplo prático e muito simples. Observe a figura abaixo:

Quero saber a menor distância entre os pontos A e B. A geometria é plana, euclidiana, a geodésica (menor distância entre 2 ponto) se chama reta e estão nas coordenadas (-4, 0) e (0, 4), respectivamente. A conta é direta:
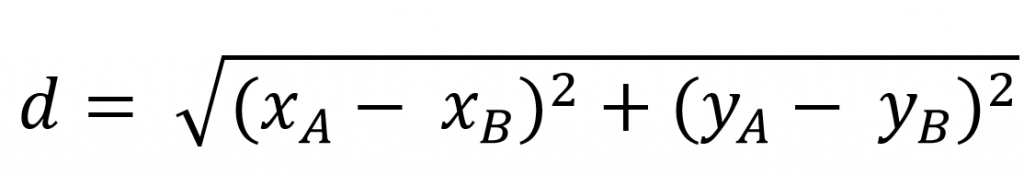
Você substitui os valores das posições de A e B na equação acima e vai encontrar o resultado (já tirado a raiz quadrada de 32) igual a 5,7 (arredondando).
Observe bem como foi escrita a equação acima. Veja que ela tem as informações das posições em X e Y de cada um dos pontos e, sem precisar levar uma trena, apenas sabendo que a geometria é plana ou euclidiana, consigo descobrir a distância entre os pontos A e B. Mas, e se a geometria não for euclidiana?
Um outro tipo de geometria que não é comum no nosso dia a dia: esférica. Agora, ao invés de você ver o mundo com retas e triângulos, imagine que as coisas fazem curvas, como se fossem curvadas, esféricas. Tente pensar que tudo a sua volta tem curvatura, como se fosse a superfície de uma bola. É claro que se a bola for muito maior do que você, a impressão que se terá é de um mundo plano: a Terra é quase que uma bola, apesar de andarmos em linhas retas por estradas e calçadas. Análogo à reta na geometria euclidiana, a geodésica na geometria esférica é o comprimento de arco:

Um exemplo visual, sem contas. Veja a figura abaixo:
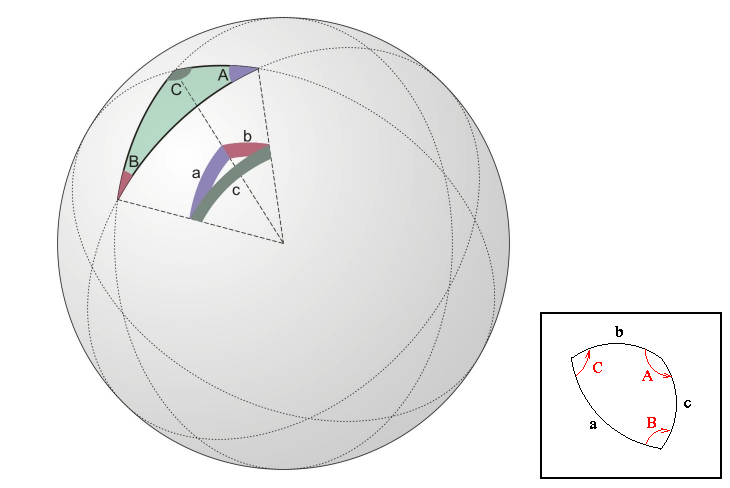
Temos aqui um triângulo em uma geometria esférica (estou expandindo o conceito que está no texto, que é apenas trigonometria esférica; muito utilizada na astronomia). Observe que a soma dos ângulos internos desse triangulo não é 180º, como é o caso na geometria euclidiana: pode observar que os ângulos são mais esparramados, espaçados. Claro que a equação (métrica) que vai nos contar como a geodésica se comporta nessa geometria euclidiana é diferente da equação mostrada acima. P.S.: para quem quiser saber como é, basta derivar da geometria riemanniana.
Toda essa curva de conversas é apenas para citar que a métrica de FLRW é uma belíssima equação que mostra como é a geodésica ou, melhor dizendo, nos conta como é a menor distância ente 2 pontos no universo. Permita-me, caro leitor, apenas deixar essa beleza estampada como forma de demonstração; não faremos contas com ela:
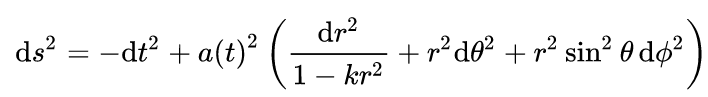
Apenas um destaque que está nessa equação: k. Essa variável nos conta como é a geometria do universo ou, melhor dizendo, nos informa se o universo é aberto, fechado ou plano (apenas e somente o universo pode ser plano; a Terra não é plana). Observe a figura abaixo:
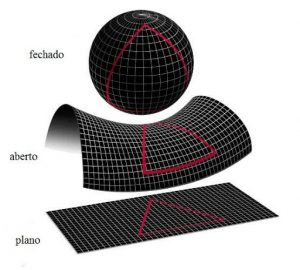
A ideia seria vivermos “imersos” nas “folhas” geométricas, ou seja, o nosso universo (casas, planetas, estrelas e galáxias) estariam nas “entranhas” da espessura dessas “folhas”, que são apenas recursos didáticos. Para cada tipo de geometria de universo há um valor de k na métrica de FLRW (1, -1 e 0, respectivamente). De acordo com as últimas medidas na radiação cósmica de fundo (CMB; falaremos em breve) o universo é plano.
Toda essa construção matemática feita pelo quarteto FLRW (todos de forma independente) tempo base o que chamamos de princípio cosmológico (não confundir com argumento cosmológico; este último é um raciocínio filosófico que tem expoentes em Aristóteles, Tomás de Aquino e recentemente por William Craig. Em suma, ele diz que tudo o que começou a existir tem uma causa e isso é aplicado ao universo). O princípio cosmológico está relacionado com a homogeneidade e a isotropia do universo em larga escala. Larga escala quer dizer distâncias acima de 300 milhões de anos-luz (1 ano-luz = 9,5 trilhões de km). Universo homogêneo e isotrópico quer dizer que ele tem a mesma aparência para todas as direções, distribuição de matéria (galáxias) é certinha (a larga escala) e não há centro: o universo não tem um centro. Novamente, parece contraintuitivo, mas futuramente esse detalhe será mais esclarecido quando falarmos sobre o início do universo.
Acredito que tem muita informação para digerir. Não se prenda, caro leitor, a equações; procure entender os conceitos que coloco aqui, da forma como estão aqui, sem grandes requintes técnicos. Seguindo esses conselhos, com toda certeza você entenderá como funciona o universo e, principalmente, que todo esse conhecimento não conflita em ponto algum com a Palavra de Deus. Ou, como diz o salmista:
A terra, ó Senhor, está cheia da tua benignidade; ensina-me os teus estatutos.
Salmos 119:64
Ficou em dúvida, quer perguntar algo ou fazer alguma crítica / sugestão? Deixe nos comentários abaixo e terei o prazer em te responder aqui ou em algum artigo específico.
Sugestão de leitura
- Sobre trigonometria esférica e aplicação à astronomia: http://astro.if.ufrgs.br/trigesf/trigesf.htm;
- O melhor material, em português, no assunto entre ciência e fé cristã é o Dicionário de cristianismo e ciência, editora Thomas Nelson Brasil em parceria com a Associação Brasileira de Cristãos na Ciência;
- Fiz mestrado e doutorado na área de cosmologia quântica. Minha dissertação e tese tem capítulo específico sobre física quântica. Também escrevi um livro, fruto da dissertação. O título da dissertação é Cosmologia quântica na gravidade teleparalela, o da tese é Discretização da energia no universo primordial e o do livro é Cosmologia quântica na gravidade teleparalela: Proposta de soluções;
- Livro Astronomia e astrofísica, por S. O. Kepler e Maria de Fátima Saraiva. Este livro é disponibilizado no próprio site dos autores, que são professores da UFRGS. É um excelente material de consulta: http://astro.if.ufrgs.br/livro.pdf;
- Livro Alfa e Ômega: a busca pelo início e fim do universo, por Charles Seife, editora Roccomn. É um livro de 2007, está um pouquinho desatualizado com relação a dados (como bóson de Higgs e ondas gravitacionais), mas ainda é muito proveitoso e com uma didática muito boa;
- Livro Cosmologia física: do micro ao macro cosmos e vice-versa, por Jorge Horvath, German Lugones, Marcelo porto, Sergio Scarano e Ramachrisna Teixeira, editora Livraria da Física. Outro livro muito bom, um pouquinho técnico, mas nada que não possa ser resolvido por si mesmo. Está um pouquinho desatualizado com relação a dados por ser de 2011, porém, altamente recomendado.

Fonte aqui