Cosmologia: lei de Hubble-Lemaître e a idade do universo
Ensina-nos a contar os nossos dias, de tal maneira que alcancemos corações sábios.
Salmos 90:12
Hoje gostaria de detalhar, ainda mais, sobre um dos temas que mais surge em dúvidas: idade do universo. Aliás, falarei sobre a lei de Hubble-Lemaître (sintetizarei sob a sigla HL), que já foi citada em outras colunas (aqui, aqui e aqui). E o motivo de voltarmos a ela é que, além de nos fornecer uma lei física (no sentido de descrição de um fenômeno), ela traz muitas informações valiosas e fundamentais sobre o universo; por exemplo, sua idade.
Como em outras colunas já falei sobre a lei de HL, inclusive sua história (aqui e aqui) e que ela é uma das evidências da teoria do Big Bang, hoje irei direto ao ponto e sua descrição, tanto matemática, como a parte prática: a constante (que pode ser “variável”; contarei sobre esse detalhe futuramente), de Hubble (H).
Começando do começo, vamos voltar lá no ensino médio (ou fundamental): função afim ou de 1º grau (para efeitos práticos, colocarei equação como sinônimo de função). A definição de função desse tipo é:
f(x) = ax + b
Onde:
- f(x) é o valor que quero encontrar (no gráfico, é a coordenada y);f(x) é o valor que quero encontrar (no gráfico, é a coordenada y);
- a é uma constante;
- x é a variável que atribuo valor;
- b é outra constante.
De maneira direta, dou valores para x e encontro y (ou f(x) ). Para isso, sempre terei os valores de a e b. Por exemplo:
f(x) = 2x + 3
- f(x) é o valor que quero encontrar;
- a é 2;
- b é 3;
- x é o valor da variável.

É simples, apenas isso: função de 1º grau, reta, corta o eixo x quando o valor de y é igual a zero etc. Agora, pegue a equação da lei de HL que já vimos anteriormente:
v = H.r.
Decompondo:
- v é o equivalente ao f(x). É o eixo y, o valor que quero encontrar. É a velocidade de uma galáxia, por exemplo;
- H é o equivalente a constante a;
- r é o equivalente ao x, o valor que dou para achar y. É a distância, de nós, até uma galáxia (por exemplo).
Ou seja, a lei de HL, que descreve o comportamento das galáxias no universo e é uma das evidências observacionais da teoria do BB é uma simples função de 1º grau.
Vamos avançar mais um passo. Sem entrar no mérito de medir distância (que é feito através do blueshift / redshift) e velocidade de objetos, a única coisa que precisamos determinar é a constante H (já que v e r são medidos por métodos específicos). E, determina-lo, é de forma direta: H = v/r, ou seja, basta dividir a velocidade v pela distância r. Ao se fazer isso com vários objetos (assim terei várias velocidades em função de seus respectivos raios) terei um gráfico com vários pontos (galáxias, supernovas Ia etc). E haverá uma reta que ligará esses pontos (com técnicas próximas de parametrização):
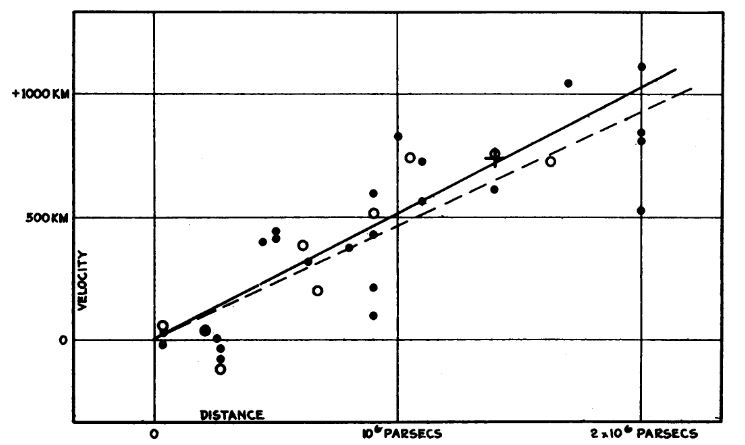
Fonte: https://www.pnas.org/content/15/3/168
Enfatizando: a obtenção desses gráficos, como esse acima feito por Hubble em 1929 (há milhares de outros), requer técnicas de observação astronômicas muito mais complicadas do que estou explicando, de forma teórica, aqui. Não é o meu propósito descrever essas técnicas observacionais, mas apenas trabalhar com os conceitos físicos e o que podemos aprender, sobre cosmologia e teologia, com eles. Em linhas gerais, meço a distância e a velocidade de afastamento (redshift) desses objetos (galáxias ou supernovas Ia) e encontro a constante de Hubble H. Há outras formas de determinação da constante de Hubble que não é por distância e velocidade de afastamento de objetos; por exemplo, olhando a radiação cósmica de fundo (CMB). Para esses casos, há outras técnicas astronômicas.

Fonte: https://arxiv.org/pdf/1811.02374.pdf
De posse da constante de Hubble H podemos, facilmente, calcular a idade do universo. Vamos lembrar de uma outra equação de física lá do 1º ano do ensino médio, mas que utilizamos constantemente no nosso dia a dia:
r = v.t
Onde:
- r é a distância percorrida (por exemplo, de uma viagem);
- v é a velocidade de um objeto (por exemplo, um carro);
- t é o tempo (por exemplo, em uma viagem).
Exemplo simples: qual é a distância percorrida (r) por um carro que anda a 100 km/h (v) durante 4 horas (t)? Basta multiplicar 100 por 4 e encontraremos a distância, r, de 400 km. Isso é usado em qualquer coisa: andando a pé, de bicicleta, carro etc. E também para objetos astronômicos. Vamos usar essa equação de distância, r, dentro da equação de HL, só que de uma forma organizada. Vamos isolar o t assim:
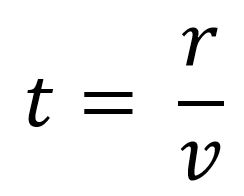
Agora, vamos puxar a equação de HL: v = H.r. Vamos jogar, na equação acima, o devido valor de v e ver o que acontece:
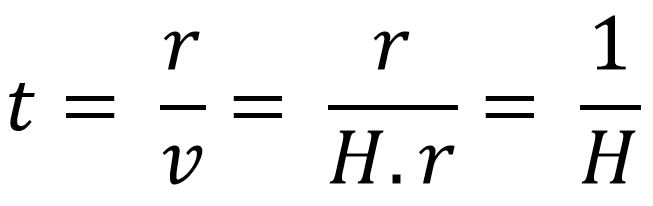
O que fiz acima foi a substituição de v por H.r e cortei o r de cima com o r de baixo (é uma fração, letras iguais são cortadas). O valor que encontrei, a fração de 1 sobre H, é chamada de tempo de Hubble: com ela consigo achar o valor da idade do universo colocando apenas o valor da constante H, que é advindo das observações astronômicas de distância e velocidade de afastamento de objetos (supernovas Ia, galáxias etc).
Parece complicado? Acho que não: utilizei apenas equações simples, que são estudadas no colégio. Mas, mesmo que você já tenha muitos anos (como eu) que terminou o ensino médio, não se preocupe: basta reler, literalmente, o que escrevi acima e você mesmo conseguirá achar a idade do universo sem ajuda. Ah, mas falta a constante de Hubble. Está aqui: 67,4 km/s/Mpc. Não se preocupe com as unidades e vamos aplicar diretamente: ao se fazer isso você chegará ao valor de, aproximadamente, 14,83 bilhões de anos. Claro que isso é uma conta direta sem os refinamentos das técnicas astronômicas; ao se fazer isso o valor mais exato da idade o universo é de 13,82 bilhões de anos (veja nos dados do satélite Planck publicados em 2018). Veja que, mesmo que o valor da constante de Hubble H e sem refinamento qualquer, podemos ter uma boa noção da idade do universo, que está na escala de 14 bilhões de anos.
Uma outra brincadeira que podemos fazer com essas equações é encontrar o quanto de distância a luz viajou, desde o nascimento do universo, até os dias atuais. A forma mais rápida de fazer essa conta é dividindo a velocidade da luz (300.000 km/s) pela constante de Hubble (67,4 km/s/Mpc). Fazendo essa conta, você achará algo do tipo 14,41 bilhões de anos-luz (1 pc = 3,24 anos-luz).
O que isso significa? Isso quer dizer que a luz, que anda a 300 mil km em 1 segundo, demorou 14 bilhões de anos, desde o nascimento do universo até os nossos dias atuais. Isso dá um tamanho de universo (desprezando que ele está crescendo) de 14 bilhões de anos-luz. Considerando que o universo está crescendo (uma das evidências da teoria do Big Bang), o tamanho do universo é de 93 bilhões de anos-luz de diâmetro (veja aqui como é feito essa análise, técnica). Ou seja, andando na velocidade da luz, a gente gastaria 93 bilhões de anos (e sem o universo se expandir) para atravessar ponta a ponta de toda a realidade física.
Acho que tem muita informação de contas e não quero chateá-lo, caro leitor, com esses dados. Vou resumir: utilizando apenas a lei de HL, aquela equação de 1º grau, obtemos a idade do universo, a velocidade de expansão (afastamento das galáxias), tamanho do universo e o seu comportamento futuro. É muita coisa que conseguimos com uma simples equação. Claro que estou desconsiderando as dificuldades técnicas e observacionais inerentes à pesquisa astronômica. Por outro lado, é mais do que o suficiente entendermos como é a dinâmica e a evolução do universo. Apesar de tudo isso, o salmista nos lembra quem é o Criador de tudo:
Antes que os montes nascessem, ou que tu formasses a terra e o mundo, mesmo de eternidade a eternidade, tu és Deus.
Salmos 90:2
Ficou em dúvida, quer perguntar algo ou fazer alguma crítica / sugestão? Deixe nos comentários abaixo e terei o prazer em te responder aqui ou em algum artigo específico.
Sugestão de leitura
- Um livro muito bom e introdutório (mas em inglês) é o Introduction to cosmology, por Barbara Ryden, 2ª ed, editora Cambridge University Press;
- Três textos, em inglês, que recomendo para entender a questão de universo observável ou tamanho do universo. Você pode utilizar o Google Translate e entender os textos, bastante simples. Há uma página da Wikipedia, mas já revisei-a e está bem coerente. https://www.space.com/24073-how-big-is-the-universe.html, http://www.bbc.com/earth/story/20160610-it-took-centuries-but-we-now-know-the-size-of-the-universe e https://en.wikipedia.org/wiki/Observable_universe;
- O melhor material, em português, no assunto entre ciência e fé cristã é o Dicionário de cristianismo e ciência, editora Thomas Nelson Brasil em parceria com a Associação Brasileira de Cristãos na Ciência;
- Fiz mestrado e doutorado na área de cosmologia quântica. Minha dissertação e tese tem capítulo específico sobre física quântica. Também escrevi um livro, fruto da dissertação. O título da dissertação é Cosmologia quântica na gravidade teleparalela , o da tese é Discretização da energia no universo primordial e o do livro é Cosmologia quântica na gravidade teleparalela: Proposta de soluções;
- Livro Astronomia e astrofísica, por S. O. Kepler e Maria de Fátima Saraiva. Este livro é disponibilizado no próprio site dos autores, que são professores da UFRGS. É um excelente material de consulta: http://astro.if.ufrgs.br/livro.pdf;
- Livro Alfa e Ômega: a busca pelo início e fim do universo, por Charles Seife, editora Roccomn. É um livro de 2007, está um pouquinho desatualizado com relação a dados (como bóson de Higgs e ondas gravitacionais), mas ainda é muito proveitoso e com uma didática muito boa;
- Livro Cosmologia física: do micro ao macro cosmos e vice-versa, por Jorge Horvath, German Lugones, Marcelo porto, Sergio Scarano e Ramachrisna Teixeira, editora Livraria da Física. Outro livro muito bom, um pouquinho técnico, mas nada que não possa ser resolvido por si mesmo. Está um pouquinho desatualizado com relação a dados por ser de 2011, porém, altamente recomendado.

Fonte: https://www.nasa.gov/feature/goddard/2016/hubble-team-breaks-cosmic-distance-record